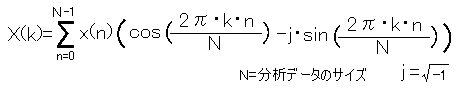音声というのは、楽器の音でもヒトの声でも、時間軸に沿った波形の強弱です。
一見すると複雑・ランダムに推移して分析などできそうもありませんが、ここで以下の仮定をします。
・音声や画像などの一見ランダムな離散データも、細かく区切って見ると周期性があるように見なせる。
ちなみに、人間の音声に関しては、それなりに根拠があるそうです。
さて、ここで離散フーリエ変換(DFT : Discrete Fourier Transform)の出番です。
詳しい説明は検索すれば沢山出てくるので、かいつまんで言うと、
・周期性のある関数は三角関数の和で表すことが出来る。
というものです。
先ほどの、細かく区切った一見ランダムでも周期性がありそうにも見える短時間のデータを一つの関数と考えるわけです。
そうすると、離散フーリエ変換(正確には短時間フーリエ変換=SDFT)を通すと、それが三角関数に分解されることになります。
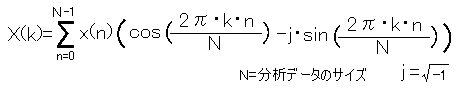
ああ、数式が出てくると途端にわけがわかりませんね。
プログラムで書くとこんな感じです。
for (int i = 0; i < size; i++)
{
for (int j = 0; j < size; j++)
{
outRe[i] += inRe[j] * Math.Cos(2.0 * Math.PI * (double)j * (double)i / (double)size);
outIm[i] -= inRe[j] * Math.Sin(2.0 * Math.PI * (double)j * (double)i / (double)size);
}
} |
ちょっと意味が変わってしましましたが、データをsizeで区切った各区間における三角関数の係数が
配列に収まっているのが分かると思います。
「データを size で区切った各区間」とは何を意味するのでしょうか。
たとえば 44100Hz でサンプリングされた音声を 2048 個集めると、約 0.0464 秒間のデータになります。
この 0.0464 秒のデータをフーリエ変換にかけると、「秒(時間域)」が「周波数域」に変換されるのです。
すなわち、44100 / 2048 = 21.533Hz を最小単位(基調波)として、その 1〜2048倍(=44100Hz) までの周波数の成分量が
sin/cos の係数として現れてきます。
数式の方を見ると分かりますが、sin の方に虚数 √-1 が入っているのでそのままでは複素数となって扱いづらいです。
プログラムの方でも、実数部(Re=Real)と虚数部(Im=Imaginary)に分けて格納しています。
これは二乗平均を取ることでパワースペクトルとして強弱を得ることができるようになるので無問題です。
いわゆるスペアナはこれを表示しているわけですね。
Spectrum[i] = Math.Sqrt(Re[i] * Re[i] + Im[i] * Im[i]);
|
|
さて、ここまでで次のことが分かるとおもいます。
・音声データをフーリエ変換にかけると、どの周波数成分が強いかが分かる。

上の図は 1Hz と 5Hzの矩形波を2つ合体させた模式図ですが、この波形がどの周波数成分を多く含むかを
調べる為にフーリエ変換を使うと 1Hz と 5Hz にパワースペクトルのピークが現れてくる、という具合です。
人間の声なども同じで、変換を使うと特徴的なピーク周波数の動きが現れてきます。
これを特にフォルマントと呼んでいるようです。
ところで、先ほど波形を三角関数に分解しましたが、逆に三角関数を寄せ集めれば元の波形になります。
これはフーリエ逆変換と言って、元の波形に戻すことが出来る変換です。
さて、三角関数・元に戻す、となるとようやく CSM 音声合成の出番です。
フーリエ変換でどの周波数が強いかが分かるわけですから、解析後の周波数を強い順にソートして、
上位いくつかをピックアップして正弦波で再現してやれば、少なくとも元の音のもっとも特徴的な部分を再現できることになります。
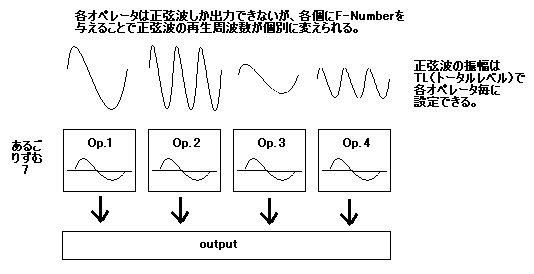
FM音源 CSM では 4 つのオペレータ(正弦波発生器)で元の波形を再現しようとするので結構無理がありそうですが、
それでもわりと聞こえる音になるのはご承知の通り。
というわけで、これで変換の説明は終わりです。
説明が冗長になるのを避けるため、書いていない部分が沢山あります。
FFT とか窓関数とか不確定性原理とか標本化定理とか離散サイン/コサイン変換とかウェーブレット変換etc,etc...
そもそも素人の筆者が書いても間違いだらけになる可能性が高いので他所で調べていただくことを強くお勧めします。
概要は上に書いた通りですが、8bit マシンとして嬉しいことといえばサイズとスピードの問題です。
仮に 8192Hz のサンプルを 256 ポイントの DFT(離散フーリエ変換、以下同)に通したとすると、
データの個数は 1 秒間に 8192 個 → 32 個になります。
正確には周波数データで 2byte、強弱のデータで 1byte、それが 4 オペレータ分なので 32*3*4=384 個になるわけですが、
ともかくデータサイズが縮むことは確かです。
加えて 8192Hz のデータを再生するためにはその周期で割り込みを駆動しなければならず、鈍足な 8bit マシンには
結構荷が重い作業になります。しかし、CSM 音声合成なら 32Hz の割り込みで良いので負担は軽くなります。
…といってもFM音源レジスタへの書き込みに、かなりの手間と Wait が掛かるので楽というわけでは有りませんが。
反対に、実装上問題のある点としては…
・FM音源の制限上、再現できない周波数が結構ある。
(再現するためにはマルチプルなどのデータを含める必要が出てくる)
F-Number で表される正弦波の再生周波数は以下の式で表されます。
Frq = F-Number * (2 ^ (Block - 1)) * (3993600 / 72) / 2 ^ 10
これにより導き出される周波数は 0Hz〜6929.948Hzまでです。
元データのサンプリングレートがいくら高くても、再現できるのはこの辺りまでの周波数となるわけです。
刻み方も飛び飛びになっているところがあったりするので、DFT で得られた代表周波数と合致しない場合があり得ます。
しかし、人間の声に限って言えば、200Hz〜4000Hzが発音域であり、サンプリング定理によって大体 8000Hz あればカバーすることができます。
(通常の喋っている時は狭く、歌う場合は音域が当然広がる。また発音域と音声の認識に必要な音域もまた異なる)
いずれにせよ、上記を念頭に置いて、元のデータのサンプリングレートと DFT にかけるポイント数をよく吟味すべきでしょう。
・FM音源の Timer は一長一短
CSM モードでは Timer-A でキーオンするのですが、そもそも Timer-A は間隔が短いです。
Timer-A(Hz) = 7987200 / (72 * (1024 - 設定値))
間隔は 108.3333Hz 〜 110933.3Hz です。
Timer-B(Hz( = 7987200 / (1152 * (256 - 設定値))
間隔は 27.08333Hz 〜 6933.333Hz です。
8192 Hzのデータを 256 ポイントの DFT に通したとすると、32 Hzの割り込み処理が必要になるのですが、
どんなに頑張っても最長 108Hz でキーオンしてしまうのでは使えません。
ということで、場合によっては CSM モードをやめて効果音モードで実装し、再生は Timer-B 割り込みか
他の割り込みリソース、または CPU によるポーリングなどを用いる必要出てくるでしょう。
この場合、当然キーオンはその都度 FM音源 I/O ポートの 0x28 をアクセスすることになります。
とまあ、こんなところでしょう。
・応 用 編
で、結局ボーカロイドは出来るの?
むかし、PC88 に歌声人(だったかな)という、SB2 にため込んだ「あいうえお」等の単発ボイスの ADPCM をつなげて
歌を歌わせるという、誰もが思いつくけど結果が容易に想像できて尻込みするという驚異のソフトがありました。
結局サンプリング音声を繋いでも速度を変えると音程が変わってしまい、継ぎ目も不自然だったりして、アラが目立ちすぎるんですよね。
イマドキの技術で補正してやれば、違った結果になるのかもしれませんが。
フォルマント発声では、そもそも周波数の集まりとしてデータを持っているので、音程を変えずに速度を変えたり
周波数成分毎の加工が出来るので、もっと応用を効かせる余地はあります。
この分野も随分研究されているようですし、一般レベルでかなりの実証とノウハウの蓄積(いわゆる調教)が進んでいるでしょうから
目標地点としても随分ハードルは高くなってしまった感があります。
ま、それ以前に素材が無いとどうしようもないんですけどね。HAHAHA
■ 反 省
直接的なきっかけとなったのは↓の動画でした。
MIDI 音源の音色 Sine Wave を 8 個使って音声合成をするというもので、
これを見た時は、その発想は無かった!まさに膝ポンでした。
音声として十分聞き取れるレベルで、データのチューニング等、色々工夫されたのだろうと思います。
MIDI の転送レートでこれだけ出来ると言うことは、データをバルクダンプしているのでしょうか。凄いです。
参考資料…あまりに多い上に理解できたとは恥ずかしくて言えないような有様なので敢えて挙げないことにします。
海外では Sine Wave Synthesis などの名称で研究されているようですね。さすがに FM音源を使ったものはなさそうでした。
そういえば、ザカリテ等のしゃべるルーチンでは、1 周期再生の度に Timer-A に違う値をいれているようです。
ひょっとして今で言うところの可変ビットレートみたいな感じだったのでしょうか。謎。
全体として、要調整というところですね。まだまだ形にすらなっていないと言うことで。猛省。
DFT だけでなく、DST などの方法も試してみたり窓サイズを調整してみたりいろいろやってみたのですが、いまひとつ。
FM音源のスペックに沿ったうまいやり方をアドバイスいただければ幸いです。できれば易しく。
▲ TOP
 人間の音声がPCで再生されるという事実が驚きを持って受け止められる時代がありました。
人間の音声がPCで再生されるという事実が驚きを持って受け止められる時代がありました。