少し前に話題になった『どうぶつしょうぎ』を PC-6001 上でも遊べるようにしてみました。
ルールのコンパクトさやスケールの手頃感など、日曜8bitプログラミングの格好の題材だと思います。
P6同人誌への投稿ネタにしようと思っていたのですが、諸々の都合で間に合わなかった（サイズも…）のでこちらでの公開となりました。

dshogi_p6.zip（テープイメージとソースコード）

要32KBです。PC-6001mk2 以降では mode 2,page 2 で立ち上げて cload run で実行します。



ゲームの成り立ちやルールについては Wikipedia などを参照してください。
とはいえ、あまりに投げっぱなしなのもアレなのでルール概略を図で描いてみました。



でもやっぱり他のサイトでルール確認推奨。

操作は大体見て分かると思いますが、カーソルキーとファンクションキー及びスペースキーを使用します。
選択状態の解除は、ESC キーです。

ルール上、特筆すべき点としては
・敵陣一段目への自ライオンの移動が封じられるケース（次の手で取られる場合）
・敵陣一段目への持ち駒からのひよこ打ちは移動も成りも出来ない。置物化。
などでしょうか。
なお、ひよこは成らないことによるメリットは全くないので敵陣一段目移動時には必ずニワトリに成ります。

どうぶつしょうぎ『風』なのは、千日手禁止を実装していないからです。
２手前までの履歴を持っておいて比較して枝刈りすれば良いはずですが、まずはちゃんと動いているか自信がないので…。

難易度を最初に選択できます。それぞれ「ヒヨコ＝２手読み」「キリン＝３手読み」「ライオン＝４手読み」です。
Min-Max法、全幅線形探索です。枝刈りは必勝時（必敗時）のみ、αβは実装していません。

「CPU が考えるとはどういうことか」について少しだけ解説したいと思います。
本格的なものは筆者には荷が重すぎるのでほんのサワリだけです。

まず、CPU は将棋のルールを知りませんし、教えて「理解」できたりもしません。
単に各駒の動ける方向=1 動けない方向=0 とエクセルのような盤面の表を持っているだけです。
ここで実験的に 2x2 の将棋もどきな盤面を用意します。CPU の手番です。



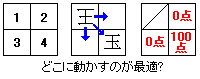
このとき、王をどこに動かすと「CPU が考えている」ように見えるでしょうか。
ルールを知っている人間からすれば直観的に 4 へ移動して玉を取るのが最善と分かるのですが、
CPU にとっては単に 3 つある手筋の 1 つにすぎません。
そこで、どの手を打つのが最善かという評価をコンピュータの得意な数値の比較に模して処理させてみることにします。

具体的には『移動した先に敵の玉があったら 100点を加算』という処理を追加することにします。
そうすると 2 と 3 に移動したときは何も取れず 0 点なのに対し、4 に移動したときは 100点加算されることになります。
移動可能な場所 (2,3,4) を全て調査して、その後の点数を比較すれば「どの手の評価が最も高いか」が分かります。

もし仮に 2 または 3 に「歩」が置かれていて取ると10点が貰えるとしても、やはり 100点貰える 4 の方が最善ということが分かります。

まずこれが基本。
ちなみに人間には自明のことですが、4 に移動しないと次の手で負けます。
これは次の手まで読まないと CPU には分かりません。
厳密に言うと上の動作も「勝ち」だから 4 へ移動したのではなく「100点だから」移動したにすぎません。
「勝ち」「負け」を評価に組み込んでいないのです。

次はさらにルールを改変して、「すべての敵駒を取ると勝ち」ということにします。
持ち駒から打つのも禁止、点数は図の左下にある通りです。



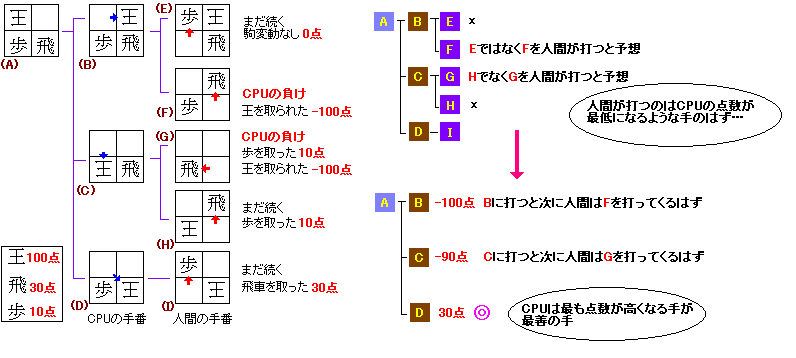
今回は 2手読みで最善の手を CPU に考えさせてみることにします。
CPU は次の手で 3カ所に打つことが出来ます。→ 盤面 (B) (C) (D)。
その次は人間の手番で、最終的に5つの盤面に分岐します。 →　盤面 (E) (F) (G) (H) (I)

このうち 2つの盤面 (B) (C)からさらに分岐する２つの盤面 (F) (G)で CPU の王が取られてしまいます。
王が取られてしまうので、点数は-100点です。

しかし (B) (C) の盤面からは (E) (H) のように、まだゲーム続行になる盤面にも分岐します。
素直に考えると、(B) あるいは (C) の盤面を前にした人間は、ほぼ間違いなく「CPU は馬鹿だなぁ」と思いつつ、(F) か (G) の手を指しますよね？
(E) (H)は無視させるべき盤面ということになりますが、 CPU にそれを正しく判断させるにはどうすればよいでしょうか。

これもまた点数の大小で判断できます。(E) ではなく(F)、(H) ではなく (G) を指すということを先の点数評価にあてはめて考えれば
「人間は CPU にとって不利な（最も点数の低い）手を打ってくるはず」となっているのが分かると思います。
（(E)=0点でなく(F)=-100点、(H)=10点でなく(G)=-90点）

ということで、2手先に人間が打ってくる手は予想できました。
これで CPU の手（1手先）の評価も確定させることができます。
すなわち、次の手で CPU が (B) (C) に打つと「王を取られる手に分岐するだろう」ということが分かったからです。
つまり(B) の盤面の点数は -100点 (C) の盤面の点数は -90点 ということになります。

さて、残った (I) の盤面ですが、これも続行盤面なのですが、30点の評価が与えられていて分岐も無いので
親盤面 (D) の点数も 30点ということになります。

最終的な盤面評価は最初の王同士の実験盤面と同じです。
CPU の手番の時は「最も点数の高い手を指すのが最善」という原則にのっとれば良いのです。
B = -100点, C = -90点, D = 30点 の中で最も高い点数は30点ですね。

これでめでたく「2手先読みした結果の最善手 = D 」を得ることができるわけです。
なお、3手読み以上も基本的に同じです。

敢えて触れませんでしたが、100点とか30点などの点数はいいかげんな数字です。
「この局面でこの駒を取るとどのくらいの評価値が得られるか」というのは本来は「評価関数」というもので算出します。
持ち駒や定石などの様々な要素を勘案して（本来であれば）算出されるべきものです。
思考ルーチンのキモになる部分であり、近年のコンピューター性能の向上・研究の進展に伴ってもの凄いことになっている…らしいです。
本稿で触れたのは極々レガシーなやりかたなのでした。

一人遊びが出来る程度に作りこんでから、さあ山場の AI を作ろうと思ったのもつかの間…。
アセンブラで再帰処理を書くのは非常に面倒くさいのですね。
C などで書いた方が圧倒的に楽かつバグも少なくできただろうと思います。SDCC 等だとちょっぴり最適化してくれたりもします。
いっそのこと C で処理を書いて合体させようかとも思ったのですが、先に作った判定処理部などとの
関数インターフェースをすりあわせるのがこれまた面倒で、結局 AI もフルアセンブラになりました。

実装には不安がありますが、うかつに最適化に走ってしまうとバグ取りがややこしいことになるので、とりあえずメンテしやすさ優先。
（しかし中途半端に自己書き換えしてたり・・・）
インデックスレジスタを多用していることもあり遅いです。５手読み以降は P6壊れたか？というくらい非常に時間がかかります。
諸々の演出などをカットしても誤差程度にしか変わりません。

LD r,(IX+B) とか ADD HL,A などの命令が無いのが実に歯がゆい。
間接アドレッシングの豊富な 6502 とかなら楽だったのだろうか。
30年以上も昔の CPU に文句を言っても仕方のないことですが。

メモリは意外と余っています。幅優先探索などにするとスタックをかなり使いそうな気もします。
実は現状でも 16KBで動くと思います。アドレス移動は必須ですが。
速くて強い（そしてメモリコストが安い）に超したことはありませんので、色々な実装を試してみるのも一興かも。

音やアニメーションアイコン、フォントなど演出面で凝りたかったのですが、前述の通り AI の挙動に自信がないのであまり手を加えられませんでした。
2008年発表のボードゲームを古いパソコンで再現、というのも燃えるところなので 80年代前半＋子供向け＝擬古風味となりました。
カセットテープのケースにコピー紙の説明書で 2800円くらいでありそうな感じがしませんか？